氮化硼片层是由氮原子和硼原子紧密堆积形成的具有二维蜂窝状结构的材料, 是合成其他维度的氮化硼纳米材料的前驱。氮化硼分子中氮和硼原子进行sp2杂化, 硼原子具有两个空的p轨道, 氮原子有两个孤对电子, 形成的共轭结构使其具有较高的稳定性。氮化硼纳米管是氮化硼片层绕中心按一定角度卷曲形成的管状结构。按照氮化硼片层的数目可以分为单壁管和多壁管。纳米管因其小尺寸效应和独特的分子结构, 使其具有优良的物理、化学性能。一维氮化硼纳米管具有较大的长径比, 使其在轴向方向的热交换能力很强, 加工过程中可通过合适的取向制备高性能各向异性热导材料[1]。
以往对纳米材料诱导高分子结晶方面的研究, 主要针对石墨烯纳米复合材料, 对氮化硼的研究相对较少。徐家壮等[2]通过对聚丙烯-纳米石墨片复合材料的结晶行为的研究证实, 纳米石墨片具有强的异相成核能力, 可以有效地诱导聚丙烯分子链形成有序的构象。王思怿等[3]比较了碳纳米管和石墨烯诱导乙烯-辛烯嵌段共聚物结晶行为, 结果表明两种纳米结构材料均可以缩短乙烯-辛烯嵌段共聚物结晶的诱导期并且能增加其结晶速率, 两种纳米结构具有较高的表面能使其均可以作为嵌段共聚物结晶的模板。但是乙烯-辛烯嵌段共聚物在石墨烯表面结晶要符合严格的片层匹配, 并且二维结构无法像一维结构那样为晶体提供足够的生长空间, 使得石墨烯的成核作用弱于碳纳米管。六方氮化硼具有层状石墨结构, 氮化硼纳米管结构类似于碳纳米管, 氮化硼纳米材料有着超强的力学性能、高的热导性能及良好的电绝缘性。片层氮化硼具有优良的热稳定性和化学稳定性使其可以应用在极端条件下, 如在高温的氧化设备中, 石墨烯的氧化温度在400~450 ℃, 而六方氮化硼在空气中的稳定温度为1 000~1 400 ℃, 此外六方氮化硼是不溶于常见酸的, 只有熔融碱和强碱溶液可以破坏六方氮化硼的纳米结构。碳纳米结构材料与氮化硼纳米结构材料均具有较高的导热率, 但是氮化硼纳米材料均是绝缘的, 因此在制备高导热绝缘纳米复合材料方面较碳纳米材料具有先天优势。实验加工方面多将氮化硼作为导热添加剂加入聚合物中来提高复合体系的导热性能[4]。牟其伍等[5]通过将氮化硼纳米管和氮化硼片层加入到环氧树脂中, 通过改变纳米材料的分散形成导热网络, 增加复合材料的导热性能。氮化硼高分子复合体系的研究在实验方面较为成熟, 但是纳米氮化硼与聚合物分子间的相互作用的理论研究尚缺乏有力支持。本文采用计算机模拟的方法从微观角度对其诱导聚乙烯(PE)结晶的机理进行了研究。
1 模型及模拟方法在构建PE分子与氮化硼纳米复合材料时, 选用链节为20的PE分子, 将100条PE分子随机分布在氮化硼纳米管(BNNT)和氮化硼纳米片层(BNNS)周围, 其中BNNT的尺寸为1.2 nm×8 nm, BNNS的尺寸为4 nm×8 nm。开始时先将体系在700 K条件下进行30 ps分子动力学运动, 使体系充分弛豫, PE分子链完全处于无序状态。然后将体系温度降低到450 K和500 K, 做进一步动力学运动, 研究结晶过程。运用可视化分子动力学(Visual Molecular Dynamics, VMD)[6]观察结晶过程中的PE分子形态变化。下图为BNNT和BNNS体系的初始模型结构。

|
图 1 PE和BNNT复合模型(左); PE和BNNS复合模型(右) Fig. 1 PE and BNNT composite model (left); PE and BNNS composite model (right) |
模拟程序采用Lammps[7]分子动力学模拟软件。运算的时间步长均为1 fs, 相互作用力的截断半径为1 nm, 运动积分采用Velocity-Verlet算法。在模拟体系的3个方向上均采用周期性边界。PE分子的模拟采用CVFF(The consistent-valence forcefield)力场[8], 纳米结构的氮化硼选用Tersoff势函数[9]进行模拟。
2 结果与讨论 2.1 PE分子在氮化硼纳米材料表面的构象演变过程图 2、图 3分别为BNNS和BNNT诱导PE分子结晶的动力学过程。随着时间的推移BNNS和BNNT都可以诱导PE分子链在纳米材料表面形成有序结构, 说明BNNS和BNNT都可以作为诱导PE分子结晶的异相成核剂。在BNNT诱导PE结晶的过程中, 刚开始PE分子无序地分布在BNNT周围, 随着时间推移, 经过2 000 ps的动力学过程, PE分子开始部分有序排列, 当时间达到4 000 ps时PE分子的取向全部平行于BNNT的轴向, PE分子的晶体生长方向是垂直BNNT轴向的, 这与碳纳米管(CNT)的规律是相一致的[10]。对于二维结构的片层BNNS, 在4 000 ps PE分子也形成了有序结构, 但是链整体的取向性没有BNNT体系中的高。

|
图 2 BNNT诱导PE分子结晶构象变化的过程 Fig. 2 Conformational changes of PE induced by BNNT (T=500 K) |

|
图 3 BNNS诱导PE分子结晶构象变化的过程 Fig. 3 Conformational changes of PE induced by BNNS (T=500 K) |
图 4为在BNNT诱导PE分子结晶过程中体系能量的变化。不同温度下体系的总能量(Etotal)呈下降趋势, 与体系中非键能量(Epair)的变化趋势是一致的。说明诱导结晶的过程是有利于体系达到稳定结构的, 这与Flory结晶热力学的预测结果是一致的[11]。
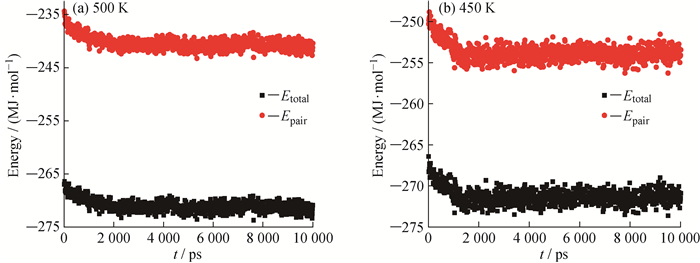
|
图 4 500 K(a)和450 K(b)时PE/BNNT复合材料体系总能量与非键能量随时间的变化过程 Fig. 4 Process of total energy and non-bond energy of PE/BNNT nanocomposites at 500 K(a) and 450 K(b) |
2.2 PE分子的键取向参数随时间的变化
为了更加深入地理解和比较BNNS和BNNT诱导PE分子结晶的机理, 引入全局键取向参数S[12]来解释结构的变化。S的表达式如下:
| $ S\text{=}\frac{1}{N\left( n-2 \right)}\sum\limits_{m-1}^{N}{\sum\limits_{i=3}^{n}{\frac{3{{\cos }^{2}}\varphi _{i}^{m}-1}{2}}} $ |
其中, N表示体系中的PE分子链条数, n表示每条分子链上骨架碳原子的个数。ψim表示第m条链当中的第i个键的向量bim与轴向所形成的角度。用bim=(rim-ri-2m )/2来表示第i个键和第i-1个键所形成的向量, rim表示第m条链的第i个原子的坐标。在考虑极端情况下, S可以取3个值, S=0时, 体系处于混乱无序的状态; S=-0.5时, 链全部垂直于所选择的轴方向; S=1.0时, 链全部平行于所选择的轴方向。
图 5, 6分别为BNNT和BNNS诱导PE结晶过程中的键取向参数变化。由图 5、6可以看出, 模拟开始时体系的链取向参数都接近于0, 体系达到了一定的无序状态。进一步对键取向参数分析可知, BNNT诱导PE结晶的速率较快。BNNT在模拟时间达到2 000 ps时, 全局键取向值就基本达到最大值(接近1.0);BNNS的诱导结晶能力相对较弱, 在4 000 ps时才可以达到平衡值(近似0.6)。说明一维材料的诱导作用比二维材料的强, 模拟的结果与Li等[13]提出的SSE软附生模型是一致的, 即成核剂的几何构型降低了分子结晶的速率, 而晶格的匹配则增加了聚合物的结晶速率。PE分子在BNNS和BNNT表面生长时, 聚合物分子链和纳米结构键遵循严格的晶格匹配原则。由于BNNT的直径相对于PE分子链的长度较小, 因此可以看成是"刚性大分子", 忽略晶格匹配的作用, 聚合物分子倾向于沿纳米管的轴向生长。而对于半径较大的BNNS结构, PE分子则表现出了多重选择性。
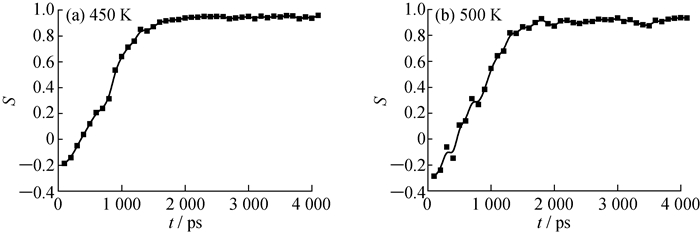
|
图 5 BNNT诱导PE结晶过程中的键取向参数变化 Fig. 5 Bond orientation parameters during the crystallization of PE induced by BNNT |
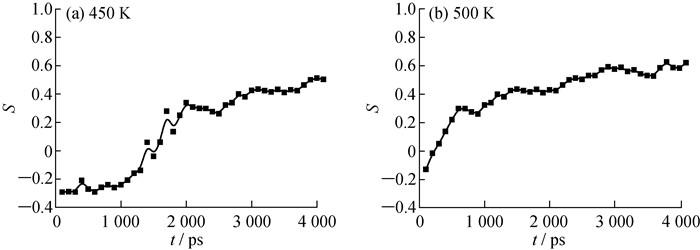
|
图 6 BNNS诱导PE结晶过程中的键取向参数变化 Fig. 6 Bond orientation parameters during the crystallization of PE induced by BNNS |
2.3 PE分子在BNNT和BNNS表面的原子分布
PE分子在BNNT和BNNS周围的密度分布函数D(r)主要用来描述沿BNNT径向方向和垂直于BNNS片层方向周围的烷烃原子的分布规律, D(r)可由如下公式计算:
| $ D\left( r \right)={{N}_{\left( r+\Delta r \right)}}/{{N}_{\text{total}}} $ |
其中:N(r+Δr)表示距离纳米管和纳米片层表面r+Δr处的原子个数, Ntotal表示体系中所有的原子数目。
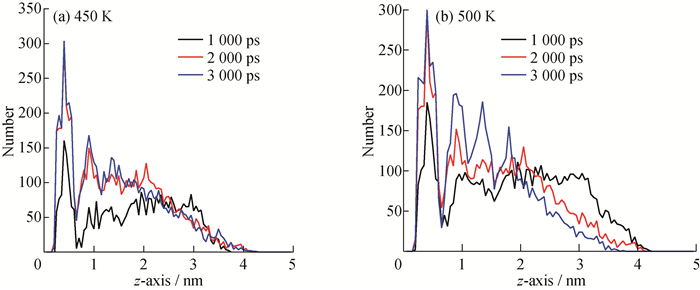
由图 7和图 8可以看出, 在沿纳米管径向方向和垂直于片层表面方向, 随着时间的变化, 远处的原子数目在减小, 近处的原子密度在增加。体系在经过700 K的高温热浴时, PE分子是随机分布的, 分布不规律, 而在1 000 ps到3 000 ps的过程中, 在BNNT体系(图 7)中可以看出PE原子在氮化硼表面的分布存在3个峰, 说明原子分布是成规律分布的; 随着时间的增长, 峰型越来越明显, 说明越来越多的PE分子有规律地分布于氮化硼表面, 这与构象观察到结果是一致的, 因为分层分布的存在, 使原子分布在几个明显的位置。
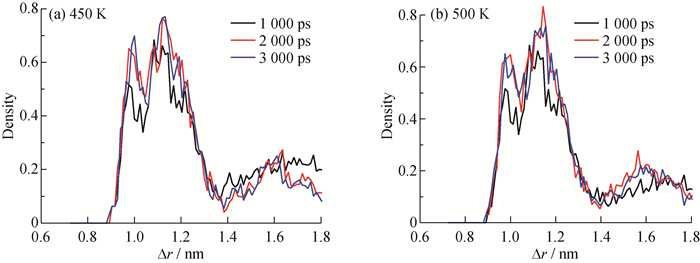
|
图 7 PE分子在BNNT表面沿径向密度分布 Fig. 7 Radial distribution of PE molecules on BNNT surface |
|
图 8 垂直于BNNS表面PE分子分布 Fig. 8 Number distribution of PE molecules perpendicular to the surface of BNNS |
由于BNNT和BNNS的极性和共轭电子效应, 强烈的分子间作用力将PE分子逐渐吸附到纳米结构表面。当越来越多的PE分子链被吸附到BNNT和BNNS表面后, 由于其与BNNT和BNNS表面的相互作用, PE分子开始逐步形成有序结构来达到稳定结构并降低分子表面能的目的。吸附与取向是相互合作的协同过程。
2.4 PE分子的扩散特性分子的构象变化与均方位移(MSD)和分子的扩散系数D(t)有密切关系。MSD的量与D(t)存在对应关系, 在3维体系中满足爱因斯坦方程:
| $ D\left( t \right) = \mathop {\lim }\limits_{t \to \infty } \frac{1}{{6t}}\left\langle {{{\left[ {r\left( {t + {t_0}} \right) - r\left( {{t_0}} \right)} \right]}^2}} \right\rangle\\ \text{MSD=}\left\langle {{\left[ r\left( t+{{t}_{0}} \right)-r\left( {{t}_{0}} \right) \right]}^{2}} \right\rangle $ |
其中:r(t0)为初始时原子的位置坐标, r(t+t0)是t+t0时刻原子的坐标。
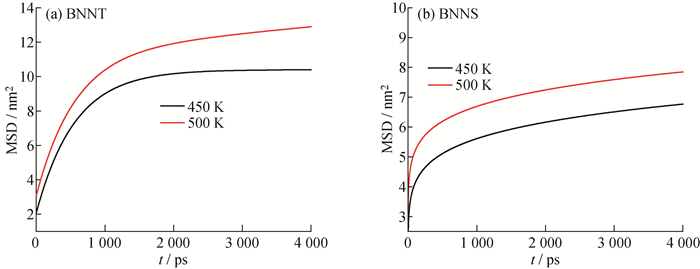
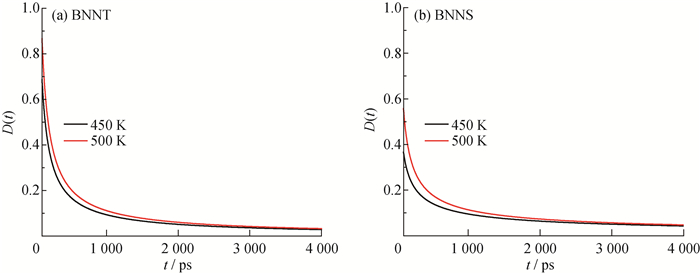
图 9、10分别为450、500 K条件下, BNNT和BNNS体系中PE分子的MSD和D(t)变化图。结果表明500 K时BNNS表面和BNNT表面的PE分子的MSD值和D(t)均高于450 K时的体系。从分子链热运动的角度看, 当温度较高时, 原子的动能较高, 分子的运动较为剧烈, 因此具有较高的MSD和D(t)。研究结果与实验观测的规律是一致的。
|
图 9 PE分子均方位移随时间的变化 Fig. 9 MSD curves of PE molecular vs time |
|
图 10 PE分子扩散系数随时间的变化 Fig. 10 Diffusion coefficient of PE molecular vs time |
通过对D(t)的分析可以看出, 经过较短时间D(t)会有一个骤降, 说明分子的运动受阻, 结合PE分子的构象演变和原子分布分析, 这是由于氮化硼纳米材料诱导PE分子结晶引起的, 由于氮化硼表面与PE分子间较强的分子间作用力, PE分子被逐渐固定在氮化硼纳米材料表面, 慢慢形成稳定有序的结构。
3 结论BNNT诱导PE烷烃分子结晶的速率明显要比BNNS的快。纳米材料由于自身维度的不同, 诱导结晶的能力也不同, 一维结构氮化硼的诱导能力远远强于二维的氮化硼片层。氮化硼纳米结构的曲率半径会影响聚合物在其表面结晶的速率。BNNS诱导结晶能力低于BNNT的原因是PE分子在氮化硼表面的多重取向, 而PE分子在BNNT表面的取向均是沿着纳米管轴向方向, 因此BNNT诱导PE分子结晶的能力和速率明显比BNNS的快。
| [1] | 段小明, 贾德昌, 周玉, 等. 织构六方氮化硼陶瓷的表征及其各向异性[C]//中国硅酸盐学会. TEIM2015第六届无机材料结构、性能及测试表征技术研讨会程序册与摘要集. 成都: 中国硅酸盐学会, 2015: 32-33. |
| [2] | 徐家壮, 唐虎, 李忠明. 低维度碳纳米填料诱导聚合物结晶[J]. 高分子通报, 2011(1): 16–23. |
| [3] | 王思怿, 郭旭虹, 陈凯敏. 聚合物刷与生物分子相互作用的研究进展[J]. 功能高分子学报, 2016, 29(4): 359–376. |
| [4] | 林杰. 基于Materials Studio的聚合物基纳米复合材料力学性能模拟[D]. 广州: 暨南大学, 2013. |
| [5] | 牟其伍, 任兵. 超细氮化硼/环氧树脂复合材料的制备和性能影响[J]. 化工新型材料, 2011, 39(4): 131–133. |
| [6] | HUMPHREY W, DALKE A, SCHULTEN K. VMD: Visual molecular dynamics[J]. Journal of Molecular Graphics, 1996, 14(1): 33–38. DOI:10.1016/0263-7855(96)00018-5 |
| [7] | PLIMPTON S, CROZIER P, THOMPSON A. LAMMPS-large-scale atomic/molecular massively parallel simulator[J]. Journal of Applied Physics, 2007, 2(20): 4740–4742. |
| [8] | ARAY Y, MURGICH J, LUNA M A. Substituent effects and the charge topology in nitriles and cyanides[J]. Journal of the American Chemical Society, 1991, 113(19): 7135–7143. DOI:10.1021/ja00019a008 |
| [9] | DODSON B W. Development of a many-body Tersoff-type potential for silicon[J]. Physical Review B, 1987, 35(6): 2795–2798. DOI:10.1103/PhysRevB.35.2795 |
| [10] | YANG J S, YANG C L, WANG M S, et al. Crystallization of alkane melts induced by carbon nanotubes and graphene nanosheets: A molecular dynamics simulation study[J]. Physical Chemistry Chemical Physics, 2011, 13(34): 15476–15482. DOI:10.1039/c1cp20695h |
| [11] | FLORY P J. Theory of crystallization in copolymers[J]. Transactions of the Faraday Society, 1955, 51: 848–857. DOI:10.1039/tf9555100848 |
| [12] | FUJIWARA S, SATO T. Molecular dynamics simulation of structural formation of short polymer chains[J]. Physical Review Letters, 1998, 80(5): 991–994. DOI:10.1103/PhysRevLett.80.991 |
| [13] | LI L, LI C Y, NI C. Polymer crystallization-driven, periodic patterning on carbon nanotubes[J]. Journal of the American Chemical Society, 2006, 128(5): 1692–1699. DOI:10.1021/ja056923h |
 2017, Vol. 30
2017, Vol. 30


