有机/无机杂化多级结构广泛存在于自然界中[1-5], 例如:存在于贝壳和珍珠中的珍珠母结构是一类以有机基质为基体、文石晶片为增强相的"砖-桥-泥"式有机/无机杂化多级结构[6-7]。这种结合了不同尺度的结构, 杂化了有机和无机成分, 常表现出比单结构、单成分材料更优异的性能。珍珠表面亮丽的色彩和昆虫翅膀绚丽的光泽都与它们内部的有机/无机杂化多级结构有关[8-9]。仿照自然界, 设计有机/无机杂化多级结构并研究其光学性能具有重要的科学意义和仿生价值[10-13]。
将多嵌段共聚物和纳米粒子共混可获得有机/无机杂化多级结构。一方面, 多嵌段共聚物可自组装形成丰富多级有序结构[14-19]。例如, Matsushita等[17]证实P(IS)4P和P(IS)2I型多嵌段共聚物可形成层中有层、层中有柱等多级结构。另一方面, 将纳米粒子引入到多嵌段共聚物中, 利用多嵌段共聚物调控纳米粒子分布, 可获得有机/无机杂化多级结构[20-22]。本课题组曾利用自洽场/密度泛函理论研究证实, 多嵌段共聚物和纳米粒子共混体系可形成纳米粒子呈多级分布的层中有层的杂化结构[20]。基于前期工作, 本文拟进一步研究该有机/无机杂化多级结构的光学性能, 以阐明多级结构对光学性能的影响。
计算机模拟是研究高分子自组装结构及其性能的重要方法, 可起到预测实验现象、阐释实验机理的作用。在结构研究方面, 耗散粒子动力学(DPD)方法是一种重要的粒子化介观模拟技术。它最早由Hoogerbrugge和Koelman提出, 已被用来模拟共聚物的自组装行为[23], 例如:Brinke等利用耗散粒子动力学模拟研究了A(BC)nBA多嵌段共聚物的自组装行为, 获得了层中有层的多级有序结构[24]。在光学性能方面, Yee在1966年提出的时域有限差分(FDTD)法是数值求解麦克斯韦方程组的一种有效方法, 它被成功地应用于自组装结构光学性能的研究[25]。Buxton等使用FDTD计算了两嵌段共聚物/纳米粒子杂化结构的光学性能, 证明通过改变聚合物/纳米粒子间相互作用可调节自组装结构的光学禁带位置和宽度[26]。
本文将结合模拟自组装结构的DPD方法和计算电磁学性能的FDTD方法, 研究A(BC)n多嵌段共聚物/纳米粒子共混体系的自组装行为及其光学性能。首先, 利用DPD方法模拟A(BC)n多嵌段共聚物/纳米粒子共混体系的自组装行为, 获得纳米粒子呈现多级分布的杂化结构。然后, 利用FDTD计算由DPD模拟获得的有机/无机杂化多级结构的光学性能。研究表明, 调整嵌段共聚物间的相互作用强度、纳米粒子的体积分数等可以调节自组装结构和纳米粒子分布, 从而获得不同的光学性能。
1 方法 1.1 用于结构模拟的耗散粒子动力学DPD是用来模拟简单或者复杂流体的动力学和流变学性能的一种计算机模拟方法, 它可以处理超出分子动力学范围的空间和时间尺度[23], 是分子动力学、格子气自动机以及朗之万动力学的结合, 遵循各向同性、伽利略不变性、质量守恒和动量守恒等原则。
在DPD模拟中, 每个粒子代表着一个链段或者以相同的方式共同运动的分子或原子集合, 它们受到软势的排斥相互作用, 并由预先定义的某种碰撞原则来进行控制。DPD粒子随时间的变化通过求解牛顿运动方程得到:
| $ \frac{\text{d}{{\mathit{\boldsymbol{r}}}_{i}}}{\text{d}t}\text{=}{\mathit{\boldsymbol{v}}_{i}}, \ \ \ {{m}_{i}}\frac{\text{d}{{\mathit{\boldsymbol{v}}}_{i}}}{\text{d}t}={\mathit{\boldsymbol{f}}_{i}} $ | (1) |
其中, ri、vi、mi和fi分别代表第i个DPD粒子的位置、速度、质量和作用力。为了简化DPD模型, DPD粒子的质量被设定为1(即一个单位)。运动方程的时间积分通过修正的velocity-Verlet算法计算[27-28]。DPD粒子i的作用力fi是一种成对的相互作用力, 其表达式为:
| $ {{f}_{i}}=\sum\limits_{j\ne i}{\left( \mathit{\boldsymbol{F}}_{ij}^{\text{C}}+\mathit{\boldsymbol{F}}_{ij}^{\text{D}}+\mathit{\boldsymbol{F}}_{ij}^{\text{R}}+\mathit{\boldsymbol{F}}_{ij}^{\text{S}} \right)} $ | (2) |
式中, FijC是非键保守力, 是一种软排斥的相互作用力, 其形式如下:
| $ \mathit{\boldsymbol{F}}_{ij}^{\text{C}}={{a}_{ij}}\sqrt{\omega \left( {{r}_{ij}} \right)}{{\widehat{\mathit{\boldsymbol{r}}}}_{ij}} $ | (3) |
其中, aij是粒子i和j间的最大排斥相互作用参数; rij=ri-rj; rij=|rij|;
| $ \omega \left( {{r}_{ij}} \right)=\left\{ \begin{align} &{{\left( 1-{{r}_{ij}}/{{r}_{c}} \right)}^{2}}\ \ \ \ \ \ \left( {{r}_{ij}} < {{r}_{c}} \right) \\ &0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( {{r}_{ij}}\geqslant {{r}_{c}} \right) \\ \end{align} \right. $ | (4) |
其中, rc是截断半径, 取值1。耗散力(FijD)是作用于具有相对运动速度的粒子间的耗散力:
| $ \mathit{\boldsymbol{F}}_{ij}^{\text{D}}=-\gamma {{\omega }^{\text{D}}}\left( {{r}_{ij}} \right)\left( {{\widehat{\mathit{\boldsymbol{r}}}}_{ij}}\centerdot {{\mathit{\boldsymbol{v}}}_{ij}} \right){{\widehat{\mathit{\boldsymbol{r}}}}_{ij}} $ | (5) |
随机力(FijR)是用以补偿因耗散力产生的动能损失的相互作用力:
| $ \mathit{\boldsymbol{F}}_{ij}^{\text{R}}=\sigma {{\omega }^{\text{R}}}\left( {{r}_{ij}} \right){{\theta }_{ij}}{{\widehat{\mathit{\boldsymbol{r}}}}_{ij}} $ | (6) |
其中, vij=vi-vj; γ是耗散系数(或者摩擦因子); σ是扰动幅度; ωD(rij)和ωR(rij)是描述耗散力FijD和随机力FijR范围的权重函数, 它们在r≥rc时为零。θij是满足高斯统计的随机涨落:
| $ \left\{ \begin{align} &\left\langle {{\theta }_{ij}}\left( t \right) \right\rangle =0 \\ &\left\langle {{\theta }_{ij}}\left( t \right){{\theta }_{kl}}\left( t' \right) \right\rangle =\left( {{\delta }_{ik}}{{\delta }_{jl}}+{{\delta }_{il}}{{\delta }_{jk}} \right)\delta \left( t-t' \right) \\ \end{align} \right. $ | (7) |
为了满足耗散涨落关系, 并让整个系统达到对应于吉布斯正则系综的平衡状态, ωD(rij)和ωR(rij)中只有一个可以被任意选择, 而另外一个可通过下式确定:
| $ {{\omega }^{\text{D}}}\left( {{r}_{ij}} \right)={{\left[{{\omega }^{\text{R}}}\left( {{r}_{ij}} \right) \right]}^{2}}=\omega \left( {{r}_{ij}} \right) $ | (8) |
而且, γ和σ须满足以下关系:
| $ {{\delta }^{2}}=2\gamma {{k}_{\text{B}}}T $ | (9) |
其中, kB和T分别为波尔兹曼常数和开尔文绝对温度。
成键的DPD粒子之间还存在着简谐弹簧力的作用, 该弹簧力(FijS)的公式为:
| $ \mathit{\boldsymbol{F}}_{ij}^{\text{S}}=C\left( 1-{{r}_{ij}}/{{r}_{eq}} \right){{\widehat{\mathit{\boldsymbol{r}}}}_{ij}} $ | (10) |
其中, C为弹簧系数; req为平衡键长。
耗散粒子动力学中的物理量均是采用"约化单位":长度、质量、时间和能量分别以rc, m, τ和kBT为单位; 时间单位(τ)可以由
模拟中, 本文构建了如图 1所示的多嵌段共聚物模型和球形纳米粒子(np)模型。A(BC)n多嵌段共聚物由A嵌段和重复的B、C嵌段组成。A、B、C嵌段分别用蓝色、绿色和红色粒子表示。np由分布在外接球半径为0.5的正二十面体12个顶点上的珠子构建而成。计算机模拟采用正则(NVT)系综, 在30×30×30的周期性立方体盒子中进行。同类DPD粒子之间相互作用参数aii取25;相互排斥的不同类DPD粒子之间相互作用参数aij取150;另外, 设置B嵌段与纳米粒子相互作用参数aBp为20, 使它们相互吸引。由于DPD粒子的数量密度为3.0, 因此DPD粒子总数为81 000。纳米粒子的体积分数用Vnp表示, 其值为0~0.25。BC嵌段的数量n设置为3。模拟迭代了足够时间使体系达到平衡状态。
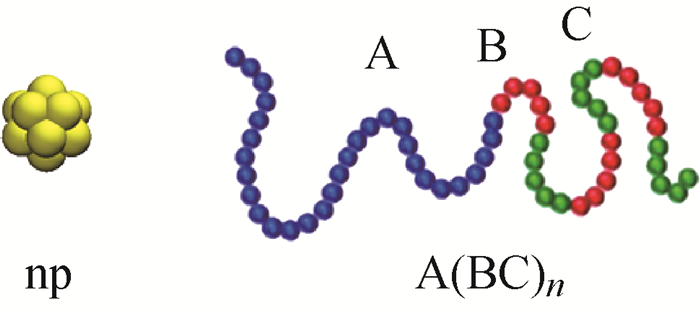
|
图 1 纳米粒子模型和A(BC)n多嵌段共聚物模型 Fig. 1 Models of the nanoparticle and A(BC)n multi-block copolymer |
1.2 用于光学性能计算的FDTD方法
FDTD是一种数值求解麦克斯韦方程的方法, 已被成功用于计算不同结构的电磁学性能。通过对电场和磁场分量在时间和空间上的交替抽样进行离散, 每一个电场分量或磁场分量周围有4个磁场分量或电场分量环绕。使用这种方式可将含有时间变量的麦克斯韦旋度方程转化为一组差分方程。边界采用完全匹配层(PML)模拟自由空间[29]。
为了进行光学性质的研究, 首先使用耗散粒子动力学模拟自组装结构, 然后根据该结构来计算FDTD中具体网格单元中心处的介电常数。介电常数(ε)通过线性加权各组分的贡献获得, 即:
| $ \varepsilon \left( \mathit{\boldsymbol{r}} \right)={{f}_{\text{A}}}\left( \mathit{\boldsymbol{r}} \right){{\varepsilon }_{\text{A}}}+{{f}_{\text{B}}}\left( \mathit{\boldsymbol{r}} \right){{\varepsilon }_{\text{B}}}+{{f}_{\text{C}}}\left( \mathit{\boldsymbol{r}} \right){{\varepsilon }_{\text{C}}}+{{f}_{\text{np}}}\left( \mathit{\boldsymbol{r}} \right){{\varepsilon }_{\text{np}}} $ | (11) |
其中:fi(r)和εi分别代表各组分在位置r处的体积分数和介电常数, i表示聚合物链段A, B, C或纳米粒子。在计算中, A、B、C嵌段的介电常数分别设为2.28, 2.53和2.28, 纳米粒子的介电常数设置为10.2, 即硒化镉的介电常数[30]。为实现模拟和实验间尺度的关联, 将多嵌段共聚物自组装形成的层状结构周期设为100 nm。为掌握光学性质对自组装形貌的依赖性, 将多级结构的周期数增加到25, 并置于介电常数等于纯链段A组分的两个均匀区域之间, 以保证照射在多层结构上时, 光的反射仅依赖于自组装结构。
2 结果与讨论 2.1 多级结构的光学性能本文首先研究了A(BC)n多嵌段共聚物自组装形成的多级结构及其光学性能。在DPD模拟中, 不同嵌段之间的相互作用参数设为aAB=aBC=aAC=150。图 2(a)所示为A(BC)n多嵌段共聚物结构的一维密度分布图, 其中小插图为相应的三维结构。蓝线和红线分别表示A和B组分的密度分布。由图可见, 多嵌段共聚物形成了层中有层的多级结构:每个大周期层中含有5个小尺度层, 包括3个小尺度B层和2个小尺度C层。
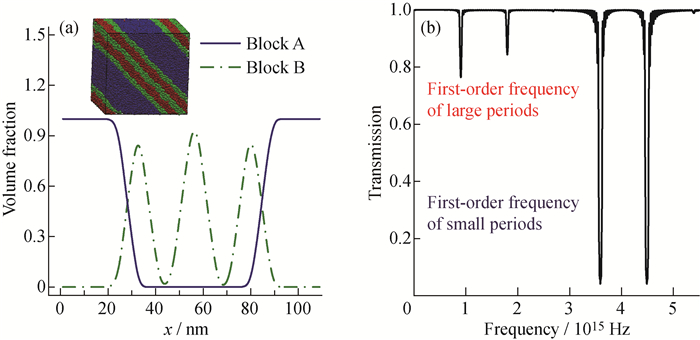
|
图 2 多级结构中A、B嵌段的一维密度分布图(a)和光透射率与频率的关系图(b) Fig. 2 Volume fraction profiles of A blocks and B blocks (a) and transmittance spectra for the hierarchical structures (b) |
多级结构将呈现出多级的反射峰特征。大尺度结构的m级反射峰频率(fm)与多级结构中大尺度周期宽度有关, 可通过理论公式估算[31]:
| $ {{f}_{m}}=\frac{{{c}_{\text{I}}}m}{2\left( {{d}_{\text{A}}}{{n}_{\text{A}}}+\sum{{{d}_{\text{B}}}{{n}_{\text{B}}}}+\sum{{{d}_{\text{C}}}{{n}_{\text{C}}}} \right)} $ | (12) |
式中, cI为光速, di为i层的宽度, ni是i组分的光学折射率, 其中i=A、B、C。由此公式估算可得, 层中有层结构的第一级反射频率为0.9×1015 Hz。类似地, 小尺度层的第一级强反射峰频率(f1)由小尺度周期的厚度决定, 表达式为:
| $ {{f}_{1}}=\frac{{{c}_{\text{I}}}}{2\left( {{d}_{\text{B}}}{{n}_{\text{B}}}+{{d}_{\text{C}}}{{n}_{\text{C}}} \right)} $ | (13) |
由于小尺度B层和C层厚度之和约为总周期厚度的1/4, 所以由此式估算的小尺度层的第一级反射峰频率是式(12) 估算的大尺度结构的4倍, 为3.6×1015 Hz。光学性能的详细信息可利用FDTD计算得到。首先, 根据图 2(a)的密度分布图和公式(11), 计算得到介电常数在多级结构中的分布; 然后, 经由FDTD计算不同频率的透射率, 计算结果如图 2(b)所以。从图 2(b)中可以看到, 第一级反射峰出现的区域与公式(12) 估算的位置基本一致; 另外, 在3.6×1015 Hz附近的强反射峰正是由公式(13) 估算的小尺度层的第一级反射峰。
由于多嵌段共聚物中各组分间的介电常数差异较小, 因此多级结构反射峰的强度和宽度都较小。增加多级结构中各组分之间的介电常数差异可增大反射峰的强度和宽度。常用的方法是在结构中引入高介电常数的纳米粒子。因此, 本文利用A(BC)n多嵌段共聚物与无机纳米粒子共混, 设计了有机/无机杂化结构, 以增强自组装结构中不同组分之间的介电常数差异, 并获得呈现多级分布结构的纳米粒子。
当纳米粒子的体积分数(
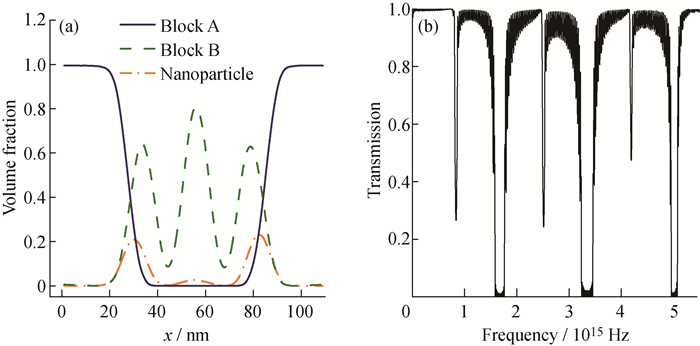
|
图 3 有机/无机杂化多级结构中A、B嵌段和纳米粒子的一维密度分布图(a)和光透射率与频率的关系图(b) Fig. 3 Volume fraction profiles of A blocks, B blocks and nanoparticles (a) and transmittance spectra for the hybrid organic/inorganic hierarchical structures (b) |
2.2 纳米粒子体积分数的影响
多嵌段共聚物与纳米粒子共混自组装形成的杂化多级结构可通过提高纳米粒子的体积分数来调控, 从而改变其光学性能。图 4为不同
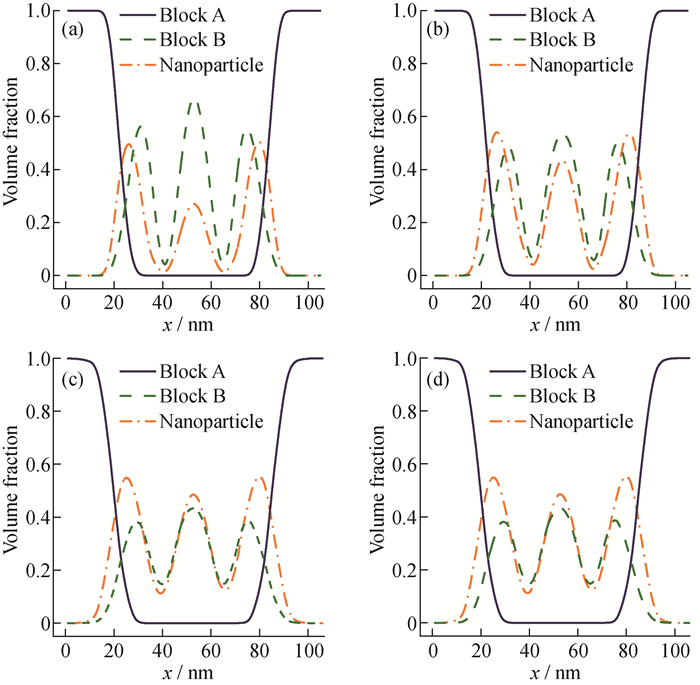
|
|
当纳米粒子在有机/无机杂化多级结构中的分布被调控后, 多级结构的光学性能也被改变。图 5为不同纳米粒子的杂化多级结构的光透射率与频率的关系图。与图 3(b)相比, 图 5(a)中的偶数级反射峰变宽; 奇数级的反射峰强度增强, 且宽度变大。图 5(b)、5(c)、5(d)中的偶数级反射峰已不再有明显变化, 而其中奇数级反射峰的强度和宽度都依次增大。结合图 4中的纳米粒子分布进行分析, 可以得出如下杂化多级结构的光学性能调控规律:奇数级反射峰的强度和峰宽可随中间B层纳米粒子含量的增加而增大, 而偶数级反射峰的强度和峰宽则随两侧B层纳米粒子含量的增加而增大。
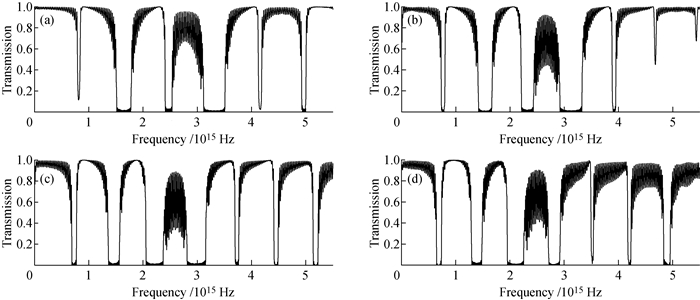
|
|
为进一步了解有机/无机杂化多级结构在可见光范围内的光学性能, 在图 6中给出了杂化多级结构对不同波长可见光的反射率。从图 6可知, 当
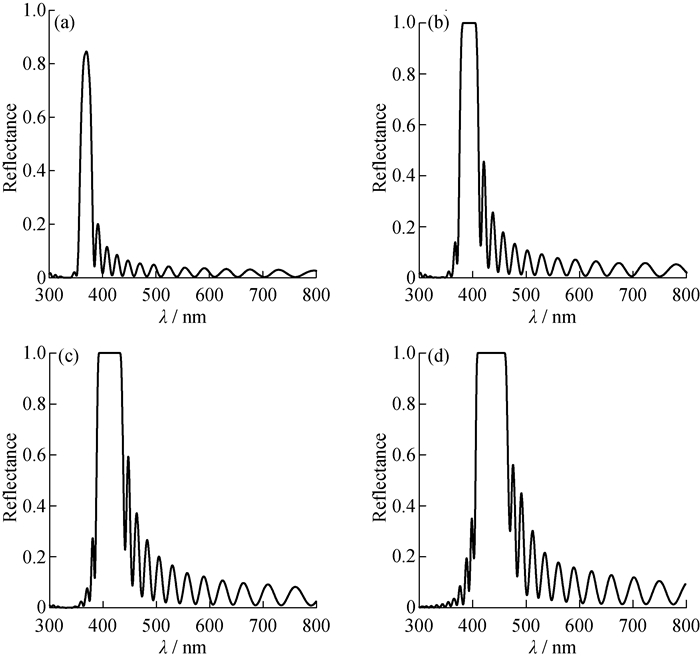
|
|
2.3 嵌段相互作用的影响
除了
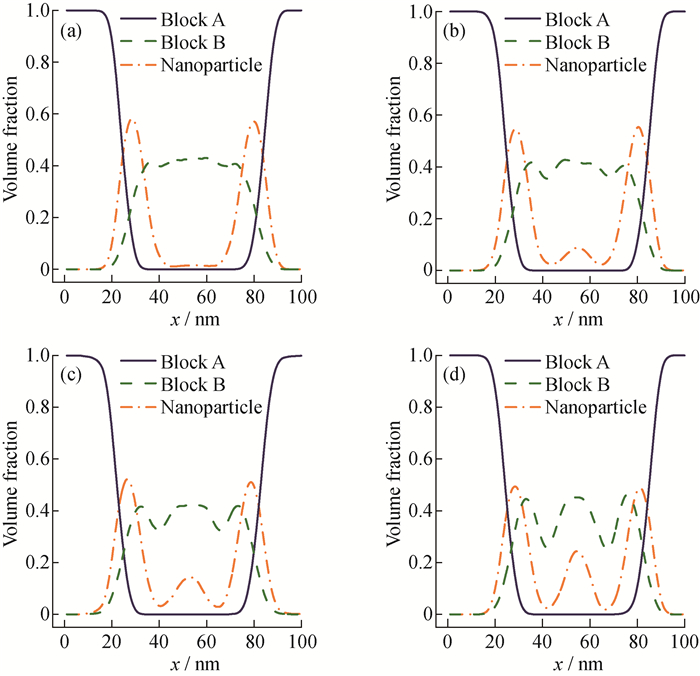
|
aBC: a—25; b—30; c—35; d—40 图 7 A、B嵌段和纳米粒子在不同相互作用参数下形成的有机/无机杂化多级结构中一维密度分布图 Fig. 7 Volume fraction profiles of A blocks, B blocks and nanoparticles for the hybrid organic/inorganic hierarchical structures with varied aBC |
在自组装结构和纳米粒子分布发生变化时, 光学性能也会发生改变。图 8为当aBC从25增加到40时, 不同频率光在多嵌段共聚物和纳米粒子共混体系自组装形成的结构中的透射率。由图 8可见, 随着aBC增加, 奇数级反射峰依次增强且宽度变大, 而偶数级反射峰基本不变。这是因为当aBC从25增加到40时, 纳米粒子含量在B、C共存相中(B、C相分离后为中间B层)逐渐增大, 使奇数级反射峰发生变化, 而纳米粒子含量在决定偶数级反射峰的B、C共存相两侧(B、C相分离后为两侧B层)中的变化较小。
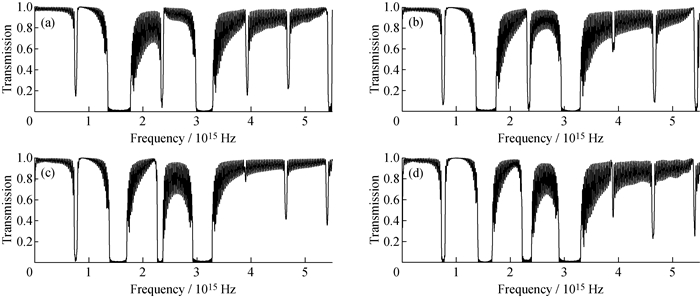
|
aBC: a—25; b—30; c—35; d—40 图 8 不同相互作用参数下形成的有机/无机杂化多级结构中的光透射率与频率的关系图 Fig. 8 Transmittance spectra for the hybrid organic/inorganic hierarchical structures with varied aBC |
不同相互作用参数aBC下, 有机/无机杂化多级结构在可见光范围内的光学性能如图 9所示。从图 9可知, 当aBC较低时(25), 所得结构为普通层状结构(见图 7(a)), 对可见光的反射能力较弱, 在波长400 nm附近有较强反射峰, 但峰高约80%, 不能全反射。当aBC增加到30时, B、C嵌段间开始有微弱的相分离, 出现了弱分离的多级结构(见图 7(b)), 反射峰仍在波长400 nm附近, 峰高虽略有增加, 但仍未达到100%。当aBC进一步增加到35时, B、C嵌段间相分离增强, 纳米粒子开始呈现多级分布(见图 7(c)), 波长400 nm处的反射峰变宽, 峰高增大到100%, 即全反射。当aBC继续增加到40时, 形成强分离的有机/无机杂化多级结构(见图 7(d)), 波长400 nm处的反射峰进一步变宽。这表明, 有机/无机杂化多级结构比普通层状杂化结构具有更强更宽的反射峰。
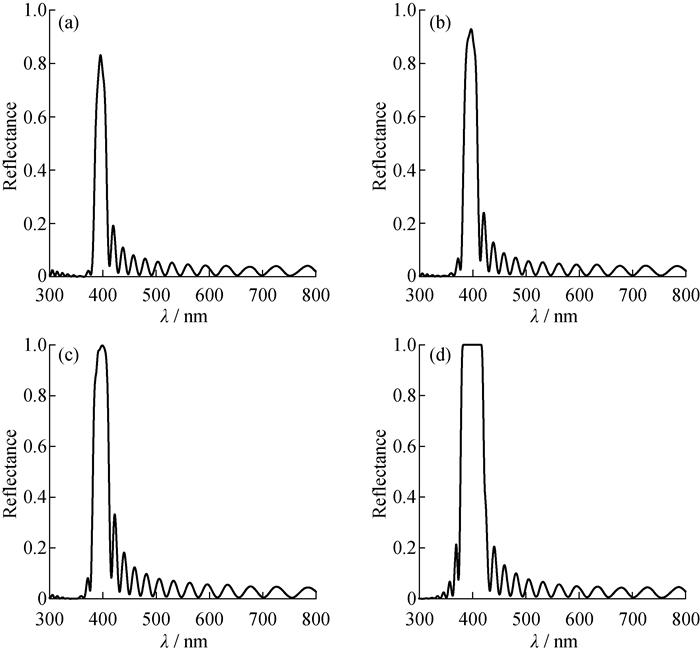
|
aBC: a—25; b—30; c—35; d—40 图 9 在不同相互作用参数下形成的有机/无机杂化多级结构中的反射率 Fig. 9 Optical reflectance spectra for the hybrid organic/inorganic hierarchical structures with varied aBC |
3 结论
多嵌段共聚物和纳米粒子共混体系可自组装形成层中有层的有机/无机杂化多级结构。与纯多嵌段共聚物形成的多级结构相比, 该多级结构具有更强更宽的反射峰。调整纳米粒子体积分数或嵌段间相互作用均可以调整有机/无机杂化的多级结构和纳米粒子的分布, 并最终调控光学性能, 如禁带位置和宽度等, 该杂化多级结构与光学性能的关系可为特定光学器件的制备提供参考。
| [1] | MAYER G. Rigid biological systems as models for synthetic composites[J]. Science, 2005, 310(5751): 1144. DOI:10.1126/science.1116994 |
| [2] | MEYERS M A, CHEN P Y, LIN A Y M, et al. Biological materials: Structure and mechanical properties[J]. Progress in Materials Science, 2008, 53(1): 1–206. DOI:10.1016/j.pmatsci.2007.05.002 |
| [3] | RITCHIE R O. The conflicts between strength and toughness[J]. Nature Materials, 2011, 10(11): 817–822. DOI:10.1038/nmat3115 |
| [4] | KINOSHITA S, YOSHIOKA S, MIYAZAKI J. Physics of structural colors[J]. Reports on Progress in Physics, 2008, 71(7): 076401. DOI:10.1088/0034-4885/71/7/076401 |
| [5] | BARTL M H, DAHLBY M R, BARROWS F P, et al. Natural photonic crystals: Formation, structure, function[J]. International Society for Optics and Photonics, 2012, 8279(1): 2. |
| [6] | WANG R Z, SUO Z, EVANS A G, et al. Deformation mechanisms in nacre[J]. Journal of Materials Research, 2011, 16(9): 2485–2493. |
| [7] | BARTHELAT F, TANG H, ZAVATTIERI P D, et al. On the mechanics of mother-of-pearl: A key feature in the material hierarchical structure[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(2): 306–337. DOI:10.1016/j.jmps.2006.07.007 |
| [8] | SEAGO A E, BRADY P, VIGNERON J P, et al. Gold bugs and beyond: A review of iridescence and structural colour mechanisms in beetles (Coleoptera)[J]. Journal of The Royal Society Interface, 2009, 6(33): S165–S184. |
| [9] | YANG W, ZHANG G P, ZHU X F, et al. Structure and mechanical properties of Saxidomus purpuratus biological shells[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2011, 4(7): 1514–1530. DOI:10.1016/j.jmbbm.2011.05.021 |
| [10] | FU Y, TIPPETS C A, DONEV E U, et al. Structural colors: From natural to artificial systems[J]. Wiley Interdisciplinary Reviews: Nanomedicine and Nanobiotechnology, 2016, 8(5): 758–775. DOI:10.1002/wnan.2016.8.issue-5 |
| [11] | ARAKAKI A, SHIMIZU K, ODA M, et al. Biomineralization-inspired synthesis of functional organic/inorganic hybrid materials: Organic molecular control of self-organization of hybrids[J]. Organic & Biomolecular Chemistry, 2015, 13(4): 974–989. |
| [12] | KAMITA G, KOLLE M, HUANG F, et al. Multilayer mirrored bubbles with spatially-chirped and elastically-tuneable optical bandgaps[J]. Optics Express, 2012, 20(6): 6421–6428. DOI:10.1364/OE.20.006421 |
| [13] | KAO J, XU T. Nanoparticle assemblies in supramolecular nanocomposite thin films: Concentration dependence[J]. Journal of the American Chemical Society, 2015, 137(19): 6356–6365. DOI:10.1021/jacs.5b02494 |
| [14] | MASUDA J, TAKANO A, NAGATA Y, et al. Nanophase-separated synchronizing structure with parallel double periodicity from an undecablock terpolymer[J]. Physical Review Letters, 2006, 97(9): 098301. DOI:10.1103/PhysRevLett.97.098301 |
| [15] | SHI L Y, PAN Y, ZHANG Q K, et al. Synthesis and self-assembly of a linear coil-coil-rod ABC triblock copolymer[J]. Chinese Journal of Polymer Science, 2014, 32(11): 1524–1534. DOI:10.1007/s10118-014-1533-7 |
| [16] | LI W, QIU F, SHI A. Emergence and stability of helical superstructures in ABC triblock copolymers[J]. Macromolecules, 2012, 45(1): 503–509. DOI:10.1021/ma2023952 |
| [17] | MASUDA J, TAKANO A, SUZUKI J, et al. Composition-dependent morphological transition of hierarchically-ordered structures formed by multiblock terpolymers[J]. Macromolecules, 2007, 40(11): 4023–4027. DOI:10.1021/ma070155s |
| [18] | WANG L, LIN J, ZHANG L. Hierarchically ordered microstructures self-assembled from A(BC)n multiblock copolymers[J]. Macromolecules, 2010, 43(3): 1602–1609. DOI:10.1021/ma902143g |
| [19] | WANG L, LIN J, ZHANG X. Hierarchical microstructures self-assembled from polymer systems[J]. Polymer, 2013, 54(14): 3427–3442. DOI:10.1016/j.polymer.2013.03.054 |
| [20] | ZHANG L, LIN J. Hierarchically ordered nanocomposites self-assembled from linear-alternating block copolymer/nanoparticle mixture[J]. Macromolecules, 2009, 42(4): 1410–1414. DOI:10.1021/ma802539q |
| [21] | DONG B, HUANG Z, CHEN H, et al. Chain-stiffness-induced entropy effects mediate interfacial assembly of Janus nanoparticles in block copolymers: From interfacial nanostructures to optical responses[J]. Macromolecules, 2015, 48(15): 5385–5393. DOI:10.1021/acs.macromol.5b01290 |
| [22] | SONG D P, LIN Y, GAI Y, et al. Controlled supramolecular self-Assembly of large nanoparticles in amphiphilic brush block copolymers[J]. Journal of the American Chemical Society, 2015, 137(11): 3771–3774. DOI:10.1021/jacs.5b01050 |
| [23] | HOOGERBRUGGE P J, KOELMAN J M V A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics[J]. EPL (Europhysics Letters), 1992, 19(3): 155. DOI:10.1209/0295-5075/19/3/001 |
| [24] | KLYMKO T, MARKOV V, SUBBOTIN A, et al. Lamellar-in-lamellar self-assembled C-b-(B-b-A)m-b-B-b-C multiblock copolymers: Alexander-de Gennes approach and dissipative particle dynamics simulations[J]. Soft Matter, 2009, 5(1): 98–103. DOI:10.1039/B809751H |
| [25] | KANE Y. Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media[J]. IEEE Transactions on Antennas and Propagation, 1966, 14(3): 302–307. DOI:10.1109/TAP.1966.1138693 |
| [26] | BUXTON G A, LEE J Y, BALAZS A C. Computer simulation of morphologies and optical properties of filled diblock copolymers[J]. Macromolecules, 2003, 36(25): 9631–9637. DOI:10.1021/ma034322+ |
| [27] | GROOT R D, WARREN P B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation[J]. The Journal of Chemical Physics, 1997, 107(11): 4423–4435. DOI:10.1063/1.474784 |
| [28] | MARTYS N S. Study of a dissipative particle dynamics based approach for modeling suspensions[J]. Journal of Rheology, 2005, 49(2): 401–424. DOI:10.1122/1.1849187 |
| [29] | BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185–200. DOI:10.1006/jcph.1994.1159 |
| [30] | EDRINGTON A C, URBAS A M, DEREGE P, et al. Polymer-based photonic crystals[J]. Advanced Materials, 2001, 13(6): 421–425. DOI:10.1002/(ISSN)1521-4095 |
| [31] | ALFREY T, GURNEE E F, SCHRENK W J. Physical optics of iridescent multilayered plastic films[J]. Polymer Engineering & Science, 1969, 9(6): 400–404. |
 2017, Vol. 30
2017, Vol. 30


